AtCoder Beginner Contest 311 参加記録 A-E
2023年07月23日
今週もAtCoder Beginner Contest 311に参加をしました。
結果
A-Eの5完、Dで3ペナでした。Highestを更新して、4桁に届いたので良かったです。
4桁行った!
— Qlitre (@kuri_tter) July 22, 2023
Qlitreさんのトヨタ自動車プログラミングコンテスト2023#4(AtCoder Beginner Contest 311)での成績:1528位
パフォーマンス:1337相当
レーティング:987→1027 (+40) :)#AtCoder #トヨタ自動車プログラミングコンテスト2023#4(ABC311) https://t.co/86YVxVoTWI
早速ですが、コンテストの振り返りを行っていきます。
A - First ABC
https://atcoder.jp/contests/abc311/tasks/abc311_a
A,B,Cからなる文字列が与えられて、最初にA,B,Cの全てが登場するのは何番目かを出力する問題です。
配列でフラグを管理する方法で解きました。
n = input()
s = input()
flg = [0, 0, 0]
for i, c in enumerate(s):
if c == 'A':
flg[0] = 1
elif c == 'B':
flg[1] = 1
else:
flg[2] = 1
# 全部出現した
if sum(flg) == 3:
print(i + 1)
exit()
B - Vacation Together
https://atcoder.jp/contests/abc311/tasks/abc311_b
N人の人の今後D日間の予定が与えられます。oなら暇、xなら予定ありです。
全員が暇な日が最大で何日間続けられるかを答える問題です。
長さDの配列を用意して、確認の予定を全探索して、駄目な日を記録するという方法をとりました。
最後に連続した箇所を数え上げます。
n, d = map(int, input().split())
al = ['o'] * d
for _ in range(n):
s = input()
for j in range(d):
if s[j] == 'x':
al[j] = 'x'
ans = 0
cnt = 0
for c in al:
if c == 'o':
cnt += 1
else:
cnt = 0
ans = max(ans, cnt)
print(ans)
C - Find it!
https://atcoder.jp/contests/abc311/tasks/abc311_c
N個の頂点とN個の辺からなる有向グラフが与えられます。
i番目の辺は頂点iから頂点Aiに伸びています。
同一頂点を複数回含まない有向閉路をひとつ求めるという問題です。
C問題で350点という少し難しいと思いました。
BFSをして既に訪れた頂点にぶつかったら、経路を復元するイメージでしょうか。
from collections import defaultdict, deque
def solve():
n = int(input())
al = list(map(int, input().split()))
graph = defaultdict(list)
for u in range(n):
v = al[u]
graph[u + 1].append(v)
vis = set()
# 一つ前に訪れた頂点
prev_nodes = [-1] * (n + 1)
# 各頂点から探索
for u in range(1, n + 1):
# 訪問済みは飛ばす
if u in vis:
continue
vis.add(u)
que = deque()
que.append(u)
# BFSする
while que:
now = que.popleft()
for ver in graph[now]:
if ver not in vis:
prev_nodes[ver] = now
que.append(ver)
vis.add(ver)
else:
# 訪問済みの場合、サイクルが発生している
lst = now
cycle = deque([lst])
end = ver
# 前に戻っていくイメージ
while True:
prev = prev_nodes[lst]
cycle.appendleft(prev)
lst = prev
if lst == end:
break
print(len(cycle))
print(*cycle)
exit()
if __name__ == '__main__':
solve()
D - Grid Ice Floor
https://atcoder.jp/contests/abc311/tasks/abc311_d
N×M のグリッドが与えられ、.は氷、#は岩をあらわします。
グリッドの外側のマスはすべて岩、プレイヤーは最初、マス (2,2)に位置しています。このマスは氷です。
プレイヤーは以下のアクションを行えます:
- 上下左右の移動方向を選択する。
- 選択した方向に、隣接するマスが岩になるまで滑って進む。岩のマスに到達した場合、移動を停止する。
このような条件で、プレイヤーが触れることができる氷のマスの数を求める問題です。
一見してBFSするだけかな?と思ったのですが、途中で訪問済みのマスにあたったとしても、探索が終わりとは限らない点が難しいです。
例えば凄く長く横に行ける氷があったとして、下から上に向かってそのマスが訪問済みになっていることがあります。
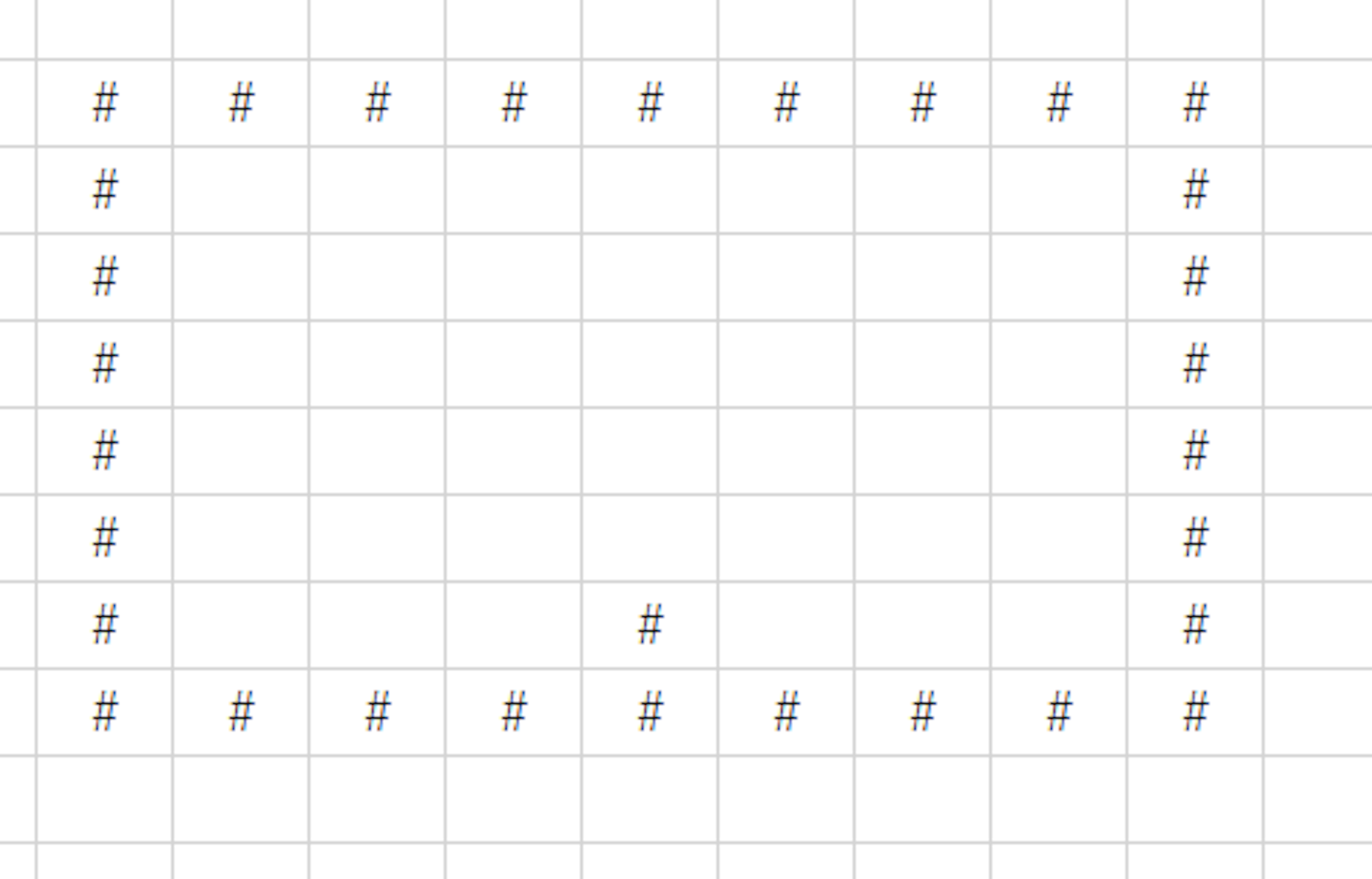
こういう図があったとして。
一番最初に下に向かってBFSしたらこういう経路になります。
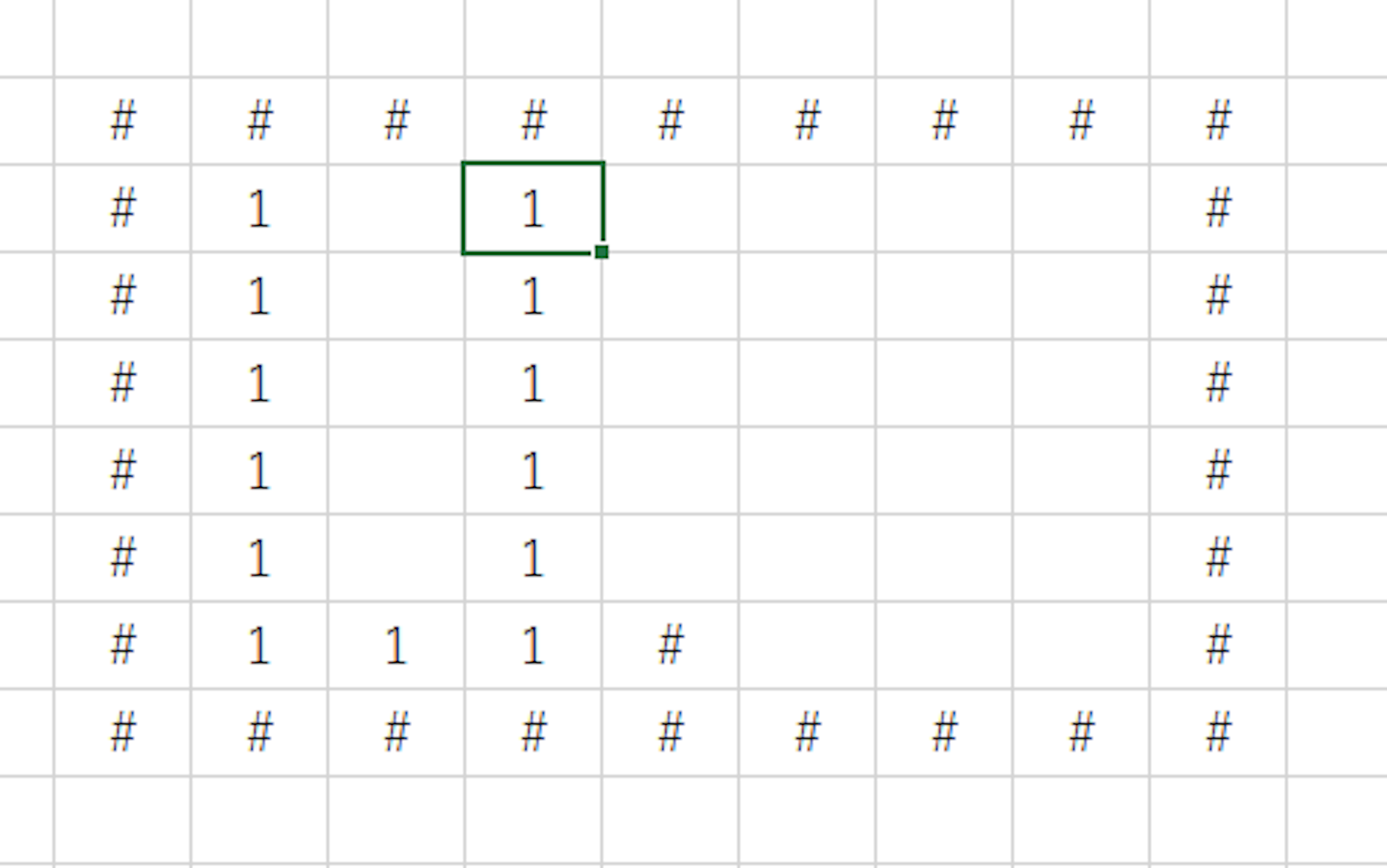
そうすると、スタート地点から横にBFSをすると、途中で訪問済みのマスにあたります。
なので、BFSでよくある訪問済みはスキップ、という手が使えません。
とはいえ、何らかの終了条件をもたせないと、永遠に探索が終わりません。かなり悩んだのですが、探索を開始するマスのみを訪問済みとしてマークをつけることで、答えが出せました。
例えば最初のマスから下に探索を開始した場合は、(1,1,'D')という情報を訪問済みとして記録します。そうして途中のマスの訪問状態は無視します。
岩にぶつかったら、今来た方向以外をキューに加える、という感じで解きました。
from collections import deque
def solve():
h, w = map(int, input().split())
grid = [list(input()) for _ in range(h)]
# 探索する方角
di_list = [('U', -1, 0), ('D', 1, 0), ('L', 0, -1), ('R', 0, 1)]
# 訪問済みの頂点
visited = [[0] * w for _ in range(h)]
# 最初は右下
que = deque([('D', 1, 1), ('R', 1, 1)])
# 探索したマスと方角を記録
searched = set()
visited[1][1] = 1
while que:
# 方角、マス
direction, r, c = que.popleft()
# 探索済みだったらcontinue
if (direction, r, c) in searched:
continue
searched.add((direction, r, c))
for di in di_list:
if di[0] == direction:
nr = r
nc = c
# 範囲内を探す
while 0 <= nr < h and 0 <= nc < w:
nr += di[1]
nc += di[2]
if grid[nr][nc] == '.':
que.append((direction, nr, nc))
visited[nr][nc] = 1
else:
# 岩にぶつかったので、一個戻って加える
# 上下に移動していた場合は左右、左右に移動していたら上下を次に加える
if direction == 'U' or direction == 'D':
ignore = 'UD'
else:
ignore = 'LR'
for char in 'UDLR':
if char in ignore:
continue
que.append((char, nr - di[1], nc - di[2]))
break
ans = 0
for al in visited:
ans += sum(al)
print(ans)
if __name__ == '__main__':
solve()
E - Defect-free Squares
https://atcoder.jp/contests/abc311/tasks/abc311_e
H x Wマスのグリッドが与えられます。
N個のa,bが与えられ、grid[a][b]は穴が開いています。
全体で穴のない正方形は何個あるか?ということを求める問題です。
まず、穴が一つも空いていない場合で、正方形が何個あるか、ということを考えます。明らかに1マスで1正方形が作れます。
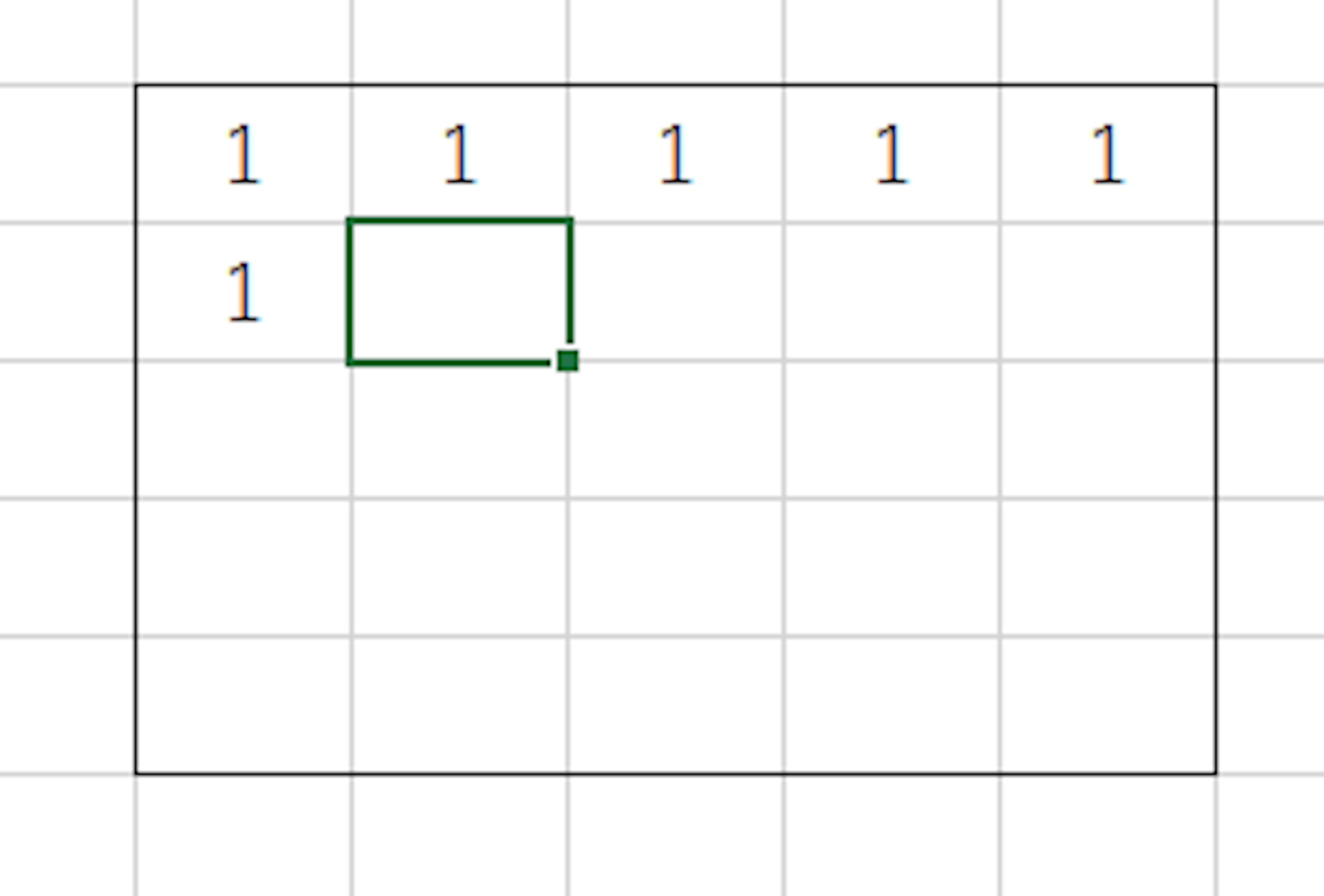
ここで、アクティブになっている箇所を考えると、左上からの領域で2 x 2の正方形がつくれます。
そのため、このマス自身と、左上を考えた場合の1個を足して、2個の正方形が作れます。
進めていくとこうなります。

このマスでは全体の一番左上から始めた場合と、一つ戻った左上から始めた場合とで、計3個の正方形が作れます。
こういう感じで埋めていくと、最終的にこうなります。
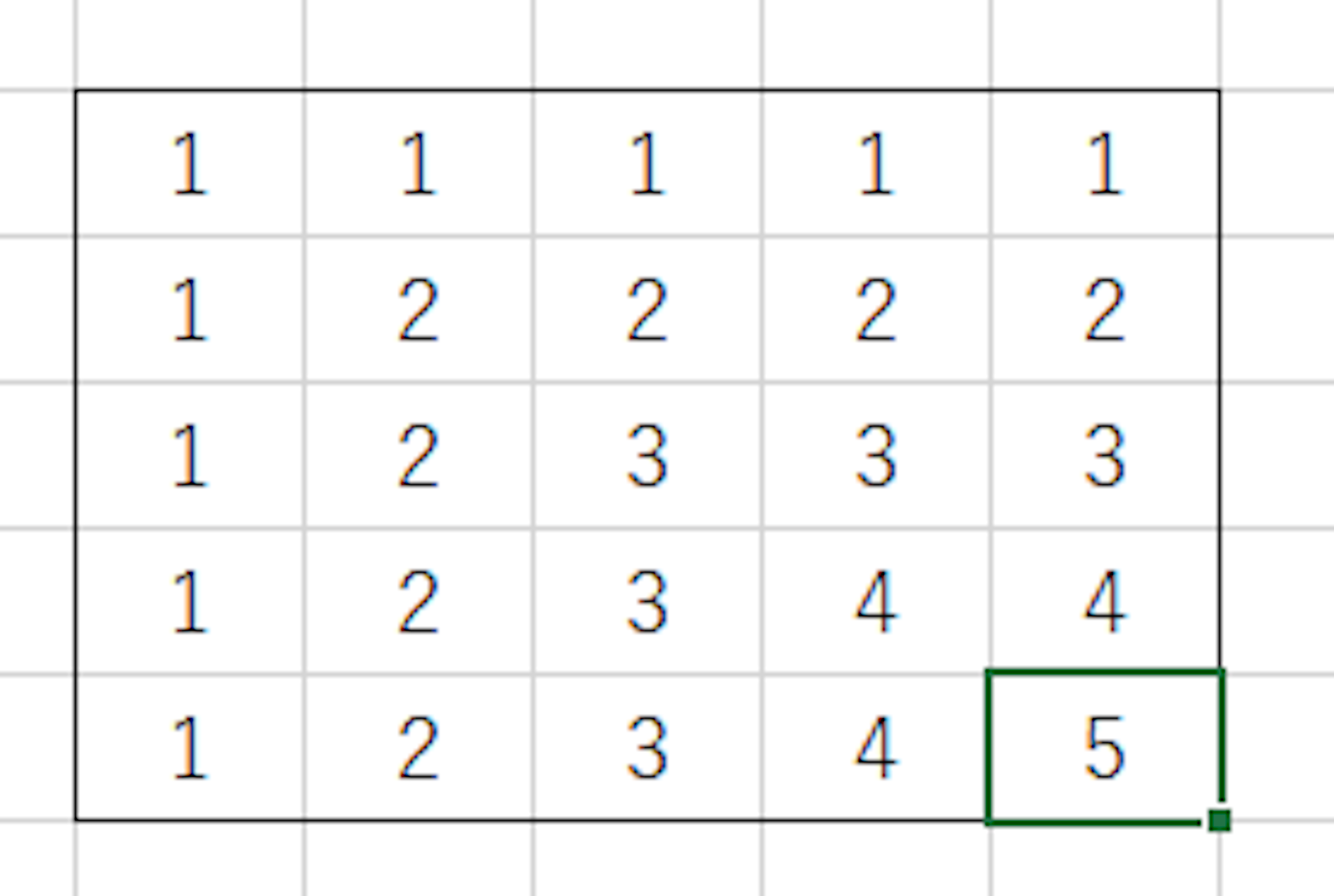
一般化すると、上、左上、左のマスの最小値+1の正方形が作れます。
穴がある場合も同様の考え方ができます。
例えば穴の箇所を0として以下のようなグリッドを考えます。

dp[i][j]、そのマスを右下としたときに作れる正方形として以下のように遷移させます。
穴が開いているマスは無視します。
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1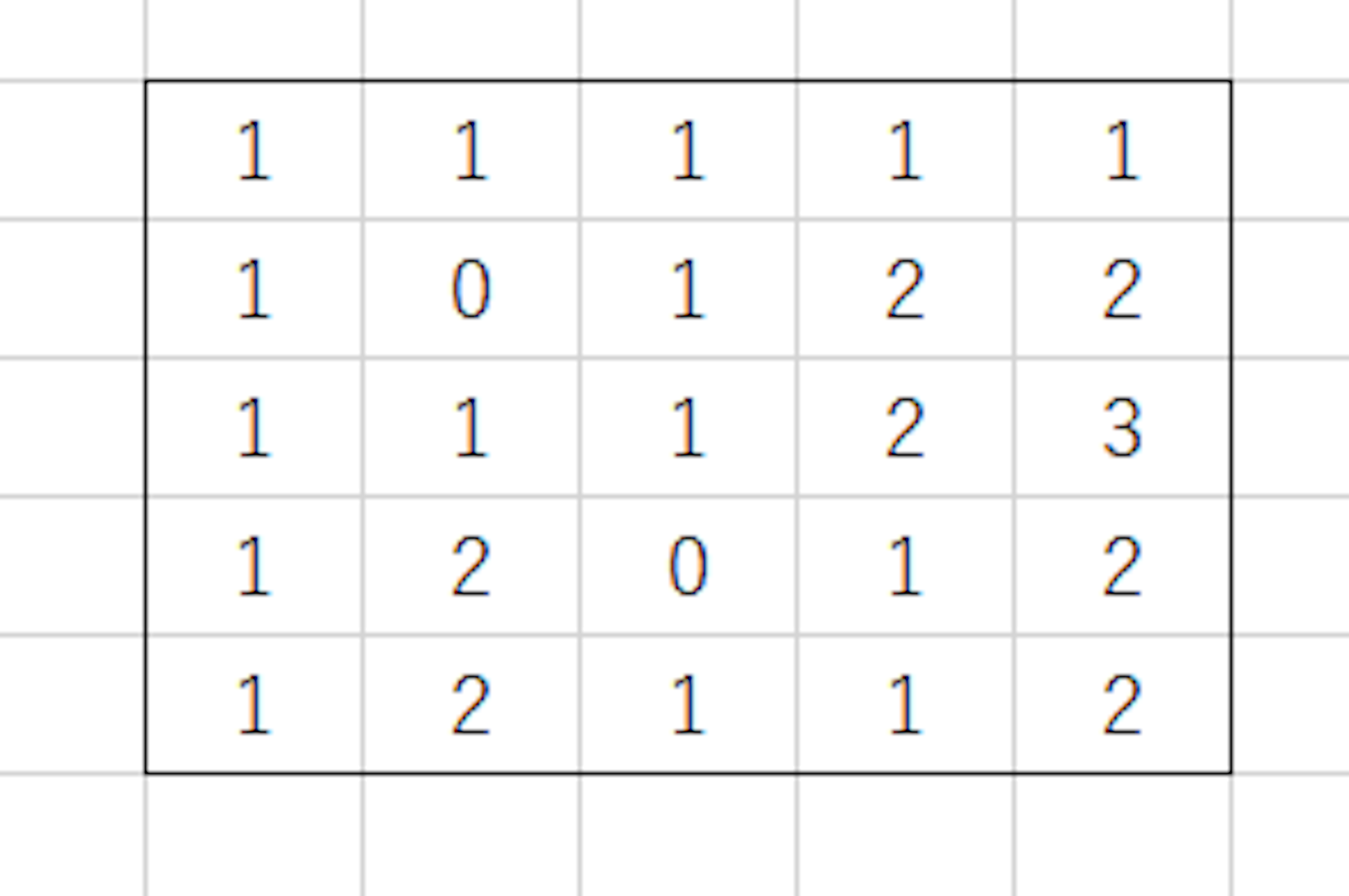
あとは足し上げれば答えです。
def solve():
h, w, n = map(int, input().split())
grid = [[1] * (w + 1) for _ in range(h + 1)]
for _ in range(n):
a, b = map(int, input().split())
grid[a][b] = 0
dp = [[0] * (w + 1) for _ in range(h + 1)]
for i in range(1, h + 1):
for j in range(1, w + 1):
if grid[i][j]:
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
ans = 0
for al in dp:
ans += sum(al)
print(ans)
if __name__ == '__main__':
solve()
おわりに
先週に3完しかできなかったのですが、今週はA-Eまで解けたのでよかったです。
BFSの問題は結構やっていたつもりなのですが、D問題でこういうのもあるのか!と驚きました。
こういう新しいパターンをしっかりと身に着けて、次回以降に素早く解けるようにしていきたいです。ではでは。
 Share
Share