AtCoder Beginner Contest 309 参加記録 A-E

2023年07月09日

今週もAtCoder Beginner Contest 309に参加をしました。

結果

A-E ５完２ペナ、2229位、1078パフォ。

Highestを更新できたのでよかった。

Qlitreさんのデンソークリエイトプログラミングコンテスト2023（AtCoder Beginner Contest 309）での成績：2229位
パフォーマンス：1078相当
レーティング：940→955 (+15) :)
Highestを更新しました！#AtCoder #デンソークリエイトプログラミングコンテスト2023（ABC309） https://t.co/THSKRLhYkE
— Qlitre (@kuri_tter) July 8, 2023

A - Nine

https://atcoder.jp/contests/abc309/tasks/abc309_a

以下のように１～９までの数字が並んでいます。

1 2 3
4 5 6
7 8 9

AとBが与えられるので、AとBが左右隣に位置しているかを判定する問題です。

上下も見てしまい１ペナを出してしまいました。

行が同じ場合でA+1 = Bを判定するのが簡単でしょうか。

a, b = map(int, input().split())

ans = 'No'

gyou_a = a // 3
if a % 3 == 0:
    gyou_a -= 1
gyou_b = b // 3
if b % 3 == 0:
    gyou_b -= 1

# 行が同じ
if gyou_a == gyou_b:
    if a + 1 == b:
        ans = 'Yes'

print(ans)

B - Rotate

https://atcoder.jp/contests/abc309/tasks/abc309_b

以下のような1と0からなるグリッドが与えられます。

このグリッドの外周のみを時計周りに回転させた結果を出力する、と言う問題です。

問題を理解するのにすこし時間がかかりました。

下の写真のようなイメージでしょうか。

外周のインデックスを予め取得しておいて、答えを埋めていく、という方法をとりました。

一発でやろうとすると、頭が混乱しそうだったので、上端→右端→下端→左端と取得しました。

n = int(input())
grid = [list(input()) for _ in range(n)]

around = []
# 上端の部分
for j in range(n):
    around.append((0, j))
# 右端の部分
for i in range(1, n - 1):
    around.append((i, n - 1))
# 下端の部分
for j in reversed(range(n)):
    around.append((n - 1, j))
# 左端の部分
for i in reversed(range(1, n - 1)):
    around.append((i, 0))

ans = [[''] * n for _ in range(n)]
# 外側を埋める
for i in range(len(around)):
    # i=0のときは最後のインデックスとなる
    prev_r, prev_c = around[i - 1]
    now_r, now_c = around[i]
    ans[now_r][now_c] = grid[prev_r][prev_c]
# 内側をうめる
for i in range(n):
    for j in range(n):
        if ans[i][j] == '':
            ans[i][j] = grid[i][j]

for row in ans:
    print(''.join(row))

C - Medicine

https://atcoder.jp/contests/abc309/tasks/abc309_c

N種類の薬があり、薬を飲む日数と錠数が与えられます。

薬は１日目から飲み始めます。飲む薬の数がK以下になるのは何日目かを出力する問題です。

一見していもす法っぽいと思いましたが、日数は10^9までと大きいので、日数のテーブルは作るとTLEします。

この手の問題は辞書型でイベントを管理して、いもす法っぽい感じで累積和を管理すると解くことができます。

from collections import defaultdict

n, k = map(int, input().split())
event = defaultdict(int)

for _ in range(n):
    a, b = map(int, input().split())
    # 1日目に+b
    event[1] += b
    # a+1日目に-bする
    event[a + 1] -= b

# 日付で並び替える
event = sorted(event.items())
# 累積和を計算
tot = 0
for i in range(len(event)):
    day, v = event[i]
    tot += v
    if tot <= k:
        print(day)
        break

D - Add One Edge

https://atcoder.jp/contests/abc309/tasks/abc309_d

N1+N2頂点数、辺の数がMのグラフが与えられます。

i番目の辺は、頂点aiと頂点biを結んでいる。
1≤u,v≤N1とN1+1≤u,v≤N1+N2を満たす全ての頂点uとvは連結している。
頂点1と頂点N1+N2は非連結であることが保証されている。

そのような中で以下の操作をします。

1≤u≤N1とN1+1≤v≤N1+N2を満たす頂点uとvを選び、それらを結ぶ新しい辺を追加する。

まとめると、頂点1と頂点N1+N2は操作後に連結になります。

その時、頂点1から頂点N1+N2までの経路の長さの最小値をdとします。

このdの最大値を求める、という問題です。

問題文が長くてややこしいですが、以下のように言い換えられます。

頂点１が属するグラフと頂点N1+N2が属するグラフがある
それぞれから頂点を一つ選び連結にする
最大距離（辺の数）を求める

明らかに頂点１から一番遠い頂点と、頂点N1+N2から一番遠い頂点を結ぶのが最大距離です。

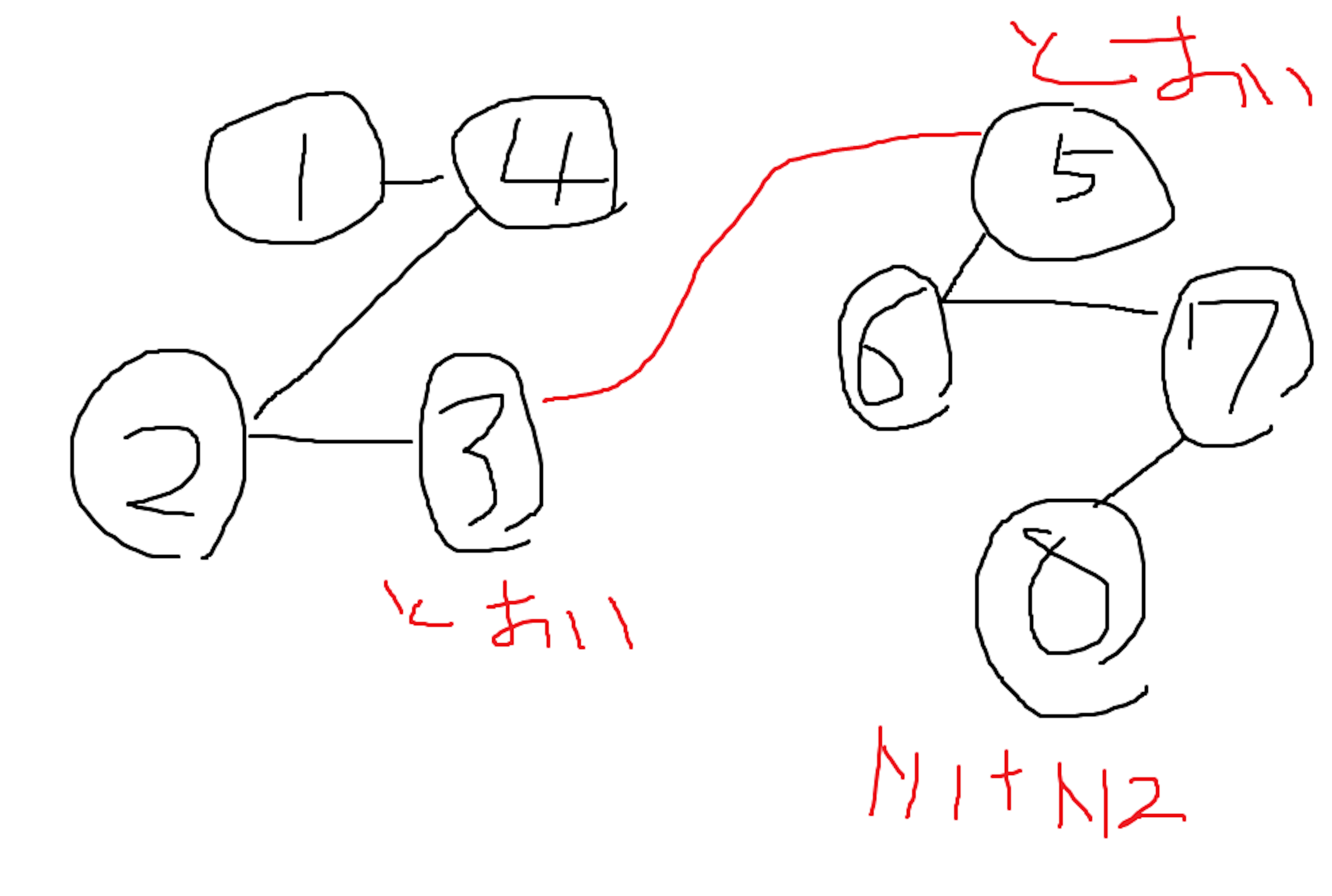
BFSを２回やってそれぞれの最大距離を足して＋１（赤い辺の部分）したものが答えです。

from collections import defaultdict, deque


def bfs(graph, start):
    """最大距離を返す"""
    max_dist = 0
    que = deque()
    que.append((start, 0))
    vis = set()
    vis.add(start)
    while que:
        now, cnt = que.popleft()
        max_dist = max(max_dist, cnt)
        for adj in graph[now]:
            if adj in vis:
                continue
            vis.add(adj)
            que.append((adj, cnt + 1))

    return max_dist


def job():
    n1, n2, m = map(int, input().split())
    graph = defaultdict(list)
    for _ in range(m):
        u, v = map(int, input().split())
        u -= 1
        v -= 1
        graph[u].append(v)
        graph[v].append(u)

    ans = bfs(graph, 0) + bfs(graph, n1 + n2 - 1)
    print(ans + 1)


job()

E - Family and Insurance

https://atcoder.jp/contests/abc309/tasks/abc309_e

人1から人Nまでの家系図の情報とM個の保険の情報が以下のように与えられます。

i>=2に対して、人iの親は人pi
i=1,2,…,Mに対して、i番目の保険の加入者は人xiで、その人自身とそのyi代先までの子孫が補償対象者となる

少なくとも1つの保険の補償対象者となる人の数を求める、という問題。

まず入力例の家系図を図にしてみます。

1 2 1 3 3 3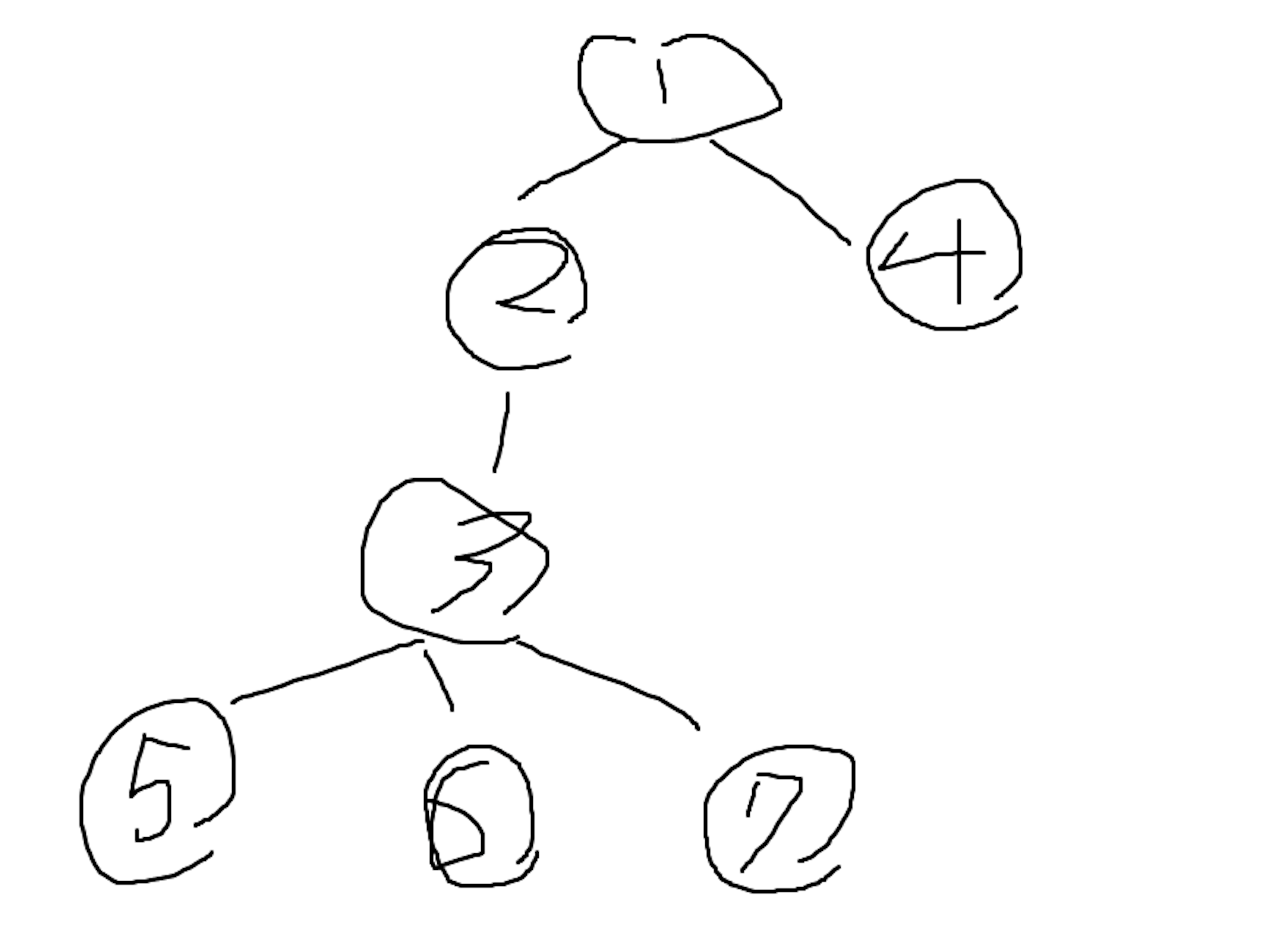

このようなときに保険の情報を加えます。Y代先まで補償できるという数字です。

入力例１とちょっと設定を変えましたが、赤字で書いてみました。

初回は保険の情報を元にBFSでつぶしていったのですが、重複して探索するパターンがどうしてもでてきます。そのため、TLEとなってしまいました。

なるべく重複しないで探索する方を考えている際に、以前に似たような問題がコンテストに出ていたことを思い出しました。

https://atcoder.jp/contests/abc305/tasks/abc305_e

ダイクストラ法を使ってYの値を更新していくことで、計算量を減らすことができました。

予めYの値をマイナス反転させておいて、子孫に行く際にカウントアップしていきます。

そうして、子孫が契約している保険のYよりも小さい場合はYの値を更新していく、という流れです。

from collections import defaultdict
import heapq


def job():
    n, m = map(int, input().split())
    parents = list(map(int, input().split()))
    graph = defaultdict(list)
    # 子孫情報を記録
    for i, parent in enumerate(parents, start=1):
        graph[parent].append(i + 1)
    # 保険情報を記録
    insurances = defaultdict(int)
    for _ in range(m):
        p, y = map(int, input().split())
        insurances[p] = max(insurances[p], y)

    inf = 10 ** 18
    # 各人が子孫に与えられる保険のパワー
    ins_power = [inf] * (n + 1)
    que = []
    for x, y in insurances.items():
        # マイナス反転させてqueに加える
        que.append((-1 * y, x))
        # 保険のパワーを更新
        ins_power[x] = -1 * y
    # heap化する
    heapq.heapify(que)

    while que:
        # パワーと親を取り出す
        now_power, parent = heapq.heappop(que)
        # これ以上子孫にパワーを与えられない
        if now_power == 0:
            continue
        for child in graph[parent]:
            # 与えられるパワー
            new_power = now_power + 1
            # 子供のパワー
            child_power = ins_power[child]
            # 与えられる場合
            if new_power < child_power:
                ins_power[child] = new_power
                heapq.heappush(que, (new_power, child))
    ans = 0
    for i in range(1, n + 1):
        if ins_power[i] < 1:
            ans += 1
    print(ans)


job()

おわりに

E問題まできっちりと解けたので満足のいく結果でした。そういえばコンテスト中にダイクストラ法を使えたのは初めてだったような気がします。

こういう「初めてできた！」みたいなことが、時々あるのが面白いところです。ではでは。

記事一覧へ